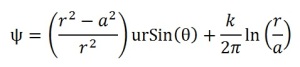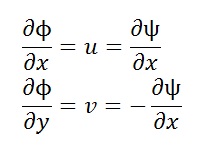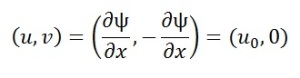This week we looked at how a fluid behaves when flowing past a cylinder with the flow being tangential to the cylinder when looked at in 2D, velocity potential and an example of its use.
Flow around a Cylinder:
In the situation stated above, we looked at a flow with stream function:
We first looked at whether you can tell that there is a cylinder from the equation and the conditions of the flow at distances far from the cylinder. We then looked at the flow velocities in polar co-ordinates, used Bernoulli’s equation to look at the flow pressure and find the stagnation pressure of the system. We found that there is relatively low pressure on the top of the cylinder and relatively high pressure on the bottom, which results in a net force pushing the cylinder upwards. Polar co-ordinates were then further used to analyse this lift and look at the drag (Which is 0 for an inviscid flow, very unrealistic).
Velocity potential:
Dealing with an ideal flow (i.e. one that is irrotational, and incompressible), we can look at the velocity potential of the flow. The flow being irrotational is what implies the existence of velocity potential. Looking at the velocity potential and stream function, we get:
These equations can then be used to find the exact form of the velocity potential.
Velocity potential example:
Looking at a uniform stream parallel to the x-axis with Speed = u0 and with:
We can find the velocity by comparing our values for u and v with the previous equations and integrating. In this case, we get equally spaced horizontal lines for the streamlines, and equally spaced vertical lines for the isopots.